Вывод преобразований Лоренца

Для термина «Лоренц» см. также другие значения.

Вы́вод преобразова́ний Ло́ренца может быть проделан многими способами, исходя из различных предпосылок.

Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым параметром $c$), как обобщение преобразований Галилея (что было проделано Пуанкаре — см. ниже). Однако впервые они были получены как преобразования, относительно которых уравнения Максвелла ковариантны (которые не меняют вида законов электродинамики и оптики при переходе к другой системе отсчёта). Преобразования можно получить из предположения их линейности и постулата одинаковости скорости света во всех системах отсчёта (являющегося упрощённой формулировкой требования ковариантности электродинамики относительно искомых преобразований, и распространением принципа равноправия инерциальных систем отсчёта (ИСО) — принципа относительности — на электродинамику), как это делается в специальной теории относительности (СТО) (при этом параметр $c$ в преобразованиях Лоренца получается определённым и совпадает со скоростью света).

Надо заметить, что если не ограничивать класс преобразований координат линейными, то первый закон Ньютона выполняется не только для преобразований Лоренца, а для более широкого класса дробно-линейных преобразований (однако этот более широкий класс преобразований — за исключением, конечно, частного случая преобразований Лоренца — не сохраняет метрику постоянной).

Алгебраический вывод

На основании нескольких естественных предположений (основным из которых является предположение о существовании максимальной скорости распространения взаимодействий) можно показать, что при смене ИСО должна сохраняться величина

$ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2},$

называемая интервалом. Из этой теоремы напрямую следует общий вид преобразований Лоренца (см. ниже). Здесь рассмотрим лишь частный случай. Для наглядности при переходе в ИСО $K'$, движущуюся со скоростью $v$, выберем в исходной системе $K$ ось $X$ сонаправленной с $v$, а оси $Y$ и $Z$ расположим перпендикулярно оси $X$. Пространственные оси ИСО $K'$ в момент времени $t=0$ выберем сонаправленными с осями ИСО $K$. При таком преобразовании

$y'=y,~~z'=z,~~c^{2}t'^{2}-x'^{2}=c^{2}t^{2}-x^{2}.$

Мы будем искать линейные преобразования Лоренца, так как при бесконечно малых преобразованиях координат дифференциалы новых координат линейно зависят от дифференциалов старых координат, а в силу однородности пространства и времени коэффициенты не могут зависеть от координат, только от взаимной ориентации и скорости ИСО.

То, что поперечные координаты не могут меняться, ясно из соображений изотропности пространства. Действительно, величина $y'$ не может изменяться и при этом не зависеть от $x$ (кроме как при вращении вокруг $v$, которое мы исключаем из рассмотрения), в чём легко убедиться подстановкой таких линейных преобразований в выражение для интервала. Но если она зависит от $x$, то точка с координатой $(0,x,0,0)$ будет иметь ненулевую координату $y'$, что противоречит наличию симметрии вращения системы относительно $v$ и изотропии пространства. Аналогично для $z'$.

Наиболее общий вид таких преобразований:

$y'=y,~~z'=z,~~ct'=ct\,\operatorname {ch} \,\alpha -x\,\operatorname {sh} \,\alpha ,~~x'=x\,\operatorname {ch} \,\alpha -ct\,\operatorname {sh} \,\alpha ,$

где $\alpha$ — некоторый параметр, называемый быстротой. Обратные преобразования имеют вид

$y=y',~~z=z',~~ct=ct'\,\operatorname {ch} \,\alpha +x'\,\operatorname {sh} \,\alpha ,~~x=x'\,\operatorname {ch} \,\alpha +ct'\,\operatorname {sh} \,\alpha .$

Ясно, что точка, покоящаяся в ИСО $K$, должна будет двигаться в ИСО $K'$ со скоростью $-v$. С другой стороны, если точка покоится, то

$dx=dx'\,\operatorname {ch} \,\alpha +c\,dt'\,\operatorname {sh} \,\alpha =0,$

${\frac {dx'}{c\,dt'}}=-{\frac {v}{c}}=-\operatorname {th} \,\alpha ~\Rightarrow ~\operatorname {th} \,\alpha ={\frac {v}{c}}.$

Учитывая, что при смене ИСО не должна меняться ориентация пространства, получим, что

$\operatorname {ch} \,\alpha \geqslant 0.$

Следовательно, уравнение для быстроты однозначно разрешимо:

$\operatorname {ch} \,\alpha ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}},~~\operatorname {sh} \,\alpha ={\frac {v}{c{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}},$

а преобразования Лоренца имеют вид

$\ x'=\gamma (x-vt),$

$\ t'=\gamma (t-{\frac {v}{c^{2}}}x),$

$\gamma =\operatorname {ch} \,\alpha ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.$

Параметр $\gamma$ называется лоренц-фактором.

Наглядный вывод преобразований Лоренца

Примем постулаты СТО, сводящиеся к расширенному принципу относительности, утверждающему, что все физические процессы протекают в точности одинаково во всех инерциальных системах отсчёта (уточняющий его принцип постоянства скорости света в СТО означает расширение принципа относительности на электродинамику вместе с уточняющим утверждением о том, что нет никакой фундаментальной физической среды (эфира), которая выделяла бы одну из систем отсчёта на опыте — то есть, если даже эфир и есть, то его наличие не должно никак нарушать принципа относительности на практике). Кроме того, полезно явно подчеркнуть, что принцип постоянства скорости света означает наличие именно конечной скорости (из эксперимента равной скорости света в вакууме), заложенной в фундаментальные законы (уравнения), одной и той же для всех инерциальных систем отсчёта, причём в каждой системе отсчёта скорость света одинакова для любых направлений его распространения и не зависит от скорости источника. Принцип постоянства скорости света составляет второй постулат СТО, который используется ниже.

Преобразование для поперечных осей (п.1)

Бильярдный шар около угловой лузы. Если бы выполнялось $y\neq y'$, шар, движущийся вдоль оси x, можно было бы забить в лузу в одних системах отсчёта и нельзя — в других

Пусть есть две бесконечные плоскости, перпендикулярные оси y. Расстояние между этими плоскостями очевидно не должно зависеть от скорости движения плоскостей вдоль самих себя, а значит — не зависит от системы отсчёта, которая движется относительно другой вдоль оси $x$. (Действительно, в каждой такой системе время прохождения луча света, движущегося вдоль оси $y$ с одной плоскости на другую, одинаково согласно постулатам СТО.)

Также можно представить, как движущееся вдоль оси $x$ тело влетает в неподвижное отверстие такого же размера. Если нет равенства $y=y',$ то в зависимости от того, в какой системе отсчёта проводится измерение, тело может быть больше или меньше отверстия. Реально же тело проходит или не проходит через отверстие независимо от выбора системы отсчёта.

То же самое, конечно, верно и для оси $z$. Поэтому, исключив для простоты физически неинтересный случай поворота на постоянный угол второй системы координат относительно первой, получаем:

$y=y',z=z'.$

Замедление времени (п.2)

Покажем, что любой процесс (например ход часов) в движущейся относительно него системе отсчета протекает медленнее, чем в его собственной системе отсчёта (относительно которой он не перемещается).

Рассмотрим «световые часы», состоящие из точечного источника и приемника света на оси $y$, удалённые друг от друга на расстояние $L$ и отмеряющие интервал времени прохождения импульса (вспышки) света от источника до приемника, равный $L/c$.

Если системы отсчета движутся относительно друг друга по оси $x$, то расстояние $L$ между двумя точками на оси $y$, измеренное в неподвижной относительно этих точек системе, такое же, как измеренное в движущейся системе отсчета, поскольку по оси $y$ нет относительного движения систем. Тем самым единицы измерения длины будут согласованы между системами. Единицы времени тоже будут согласованы, поскольку согласованы единицы длины, а скорость света не зависит от системы координат.

Таким образом, в каждой системе отсчета можно установить одинаковые световые часы.

Сравним интервал времени прохождения импульса в системе отсчета, где световые часы покоятся, и интервал времени тех же часов, измеренный идентичными часами в движущейся системе отсчета.

Пусть световые часы покоятся в системе отсчёта $K$ (левая диаграмма на рисунке), а система отсчёта $K'$ движется вправо вдоль оси $x$ со скоростью $V$. Источник в момент излучения импульса находится в начале координат A системы отсчёта $K$ (красная точка на рис.), а приёмник — в точке B (синяя) на оси $y$. В системе отсчёта $K$ испущенный импульс света достигает приёмника B на оси $y$ за время $\Delta t=L/c$.

В системе же отсчёта $K'$ импульс света излучается из начала координат в момент его совпадения с началом координат системы $K$ (точкой A), а попадает в приёмник B через время $\Delta t'=L'/c$, которое измеряется часами, движущимися вместе с системой $K'$. Координата $x'$ точки B — смещение, обозначенное на правой диаграмме на рисунке пунктиром, равно $-V\Delta t'$, точка A указывает место, откуда был излучён импульс, траектория импульса в $K'$ изображена зеленой линией.

Поскольку скорость света в любой инерциальной системе отсчёта одинакова (не зависит от скорости источника и направления излучения), источник A в момент импульса можно считать неподвижным в системе отсчёта $K'$.

Путь $L'$, пройденный импульсом света от A к B в системе отсчёта $K'$, равен гипотенузе прямоугольного треугольника. По теореме Пифагора

${\displaystyle L'^{2}}=L^{2}+(V\Delta t')^{2},$

учитывая, что ${\displaystyle L'}=c\Delta t'$и $L=c\Delta t$, найдём выражение для $\Delta t'$

$\Delta t'={\frac {\Delta t}{\sqrt {1-{\frac {V^{2}}{c^{2}}}}}}.$

Отсюда следует, что $\Delta t'>\Delta t$ при $V\neq 0.$

Таким образом, интервал времени $\Delta t'$ любого процесса, происходящего в системе отсчёта $K$, измеренный часами в движущейся системе отсчета $K'$, больше, чем интервал времени $\Delta t$, измеренный такими же часами в собственной системе отсчёта $K$. Коэффициент увеличения интервала постоянен при постоянной скорости.

Поскольку система отсчёта $K$ движется относительно системы $K'$ со скоростью $-V$, то говорят, что время в движущейся системе отсчёта $K$ с точки зрения системы $K'$ течёт замедленно. Например, лабораторное время жизни $\Delta t'$ короткоживущих частиц, рождающихся с большими скоростями, больше их времени жизни $\Delta t$ в собственной системе отсчёта.

Более наглядно замедление времени проявляется в замедлении хода (темпа) часов, движущихся вместе с системой отсчёта $K$. Если источник и приёмник снабдить зеркалами, отражающими световой импульс, то интервал любой длительности можно измерять числом периодов между отражениями. Частота колебаний такого светового маятника характеризует скорость течения времени. Период $T$ повторяющегося процесса связан с его частотой равенством $\nu ={\frac {1}{T}}$. Большему периоду соответствует меньшая частота, и неравенство $\Delta t'>\Delta t$ переходит в неравенство для частоты $\nu '<\nu$, где $\nu '$ — частота светового маятника часов, движущихся вместе с системой $K$, измеренная часами системы $K'$, $\nu$ — частота светового маятника в собственной системе отсчёта $K$ (относительно которой часы покоятся). Движущиеся часы тикают реже, чем неподвижные.

Поскольку все инерциальные системы отсчёта равноправны, то, измеряя длительность прохождения импульса в часах, движущихся вместе с системой отсчёта $K'$, часами системы отсчёта $K$, получим обратное неравенство $\Delta t'<\Delta t$ при $V\neq 0$, так как в этом случае $\Delta t'$ является собственным временем. С точки зрения системы отсчёта $K$ движущиеся часы системы $K'$ идут медленнее собственных часов системы $K$.

Относительность одновременности (п.3)

Изменение времени на неподвижных звёздах в системе отсчёта движущегося космического корабля. Когда мы около Земли, время изменяется на Веге, и наоборот. В результате не возникает парадокс близнецов

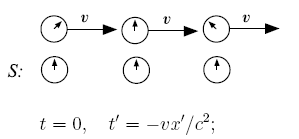
Кроме замедления времени в движущейся системе отсчёта (замедления хода всех часов в движущейся лаборатории по сравнению с ходом часов в неподвижной лаборатории), оказывается, что начало отсчёта времени в движущейся системе отсчёта также не совпадает с таковым в неподвижной, причем сдвиг этого начала отсчёта — разный в различных точках — зависит от x. Часы в своей собственной системе отсчёта, показывающие одинаковое время, показывают разное опережение/отставание, зависящее от их расположения, если на них смотреть из системы отсчёта, относительно которой их собственная система отсчёта движется.

Чтобы стало понятным само существо проблемы, придется так или иначе обдумать вопрос, а что значит, что часы в разных удалённых друг от друга точках пространства (например, в разных городах) идут одинаково (синхронно), как в этом можно убедиться, или как (с помощью какой процедуры) можно синхронизировать часы в разных местах, если изначально они не были синхронны.

Уже простейший способ синхронизации, заключающийся в том, что все часы синхронизируют в одном месте, а затем их переносят в разные точки, позволяет убедиться в том, что часы, синхронизированные в одной системе отсчёта, будут выглядеть показывающими разное время из другой системы отсчёта. Дело в том, что для часов, которые мы переносим в разные точки по оси x, их скорость относительно другой системы отсчёта будет обязательно различной, поэтому время в разных точках оси x будет сдвинуто по-разному.

Это можно было бы аккуратно рассмотреть количественно, получив таким образом искомый результат. Но более просто этого достичь позволяет рассмотрение синхронизации с помощью световых сигналов (а принцип относительности говорит, что любой корректный способ синхронизации должен дать один и тот же результат, в чём, впрочем, при желании можно убедиться и явно).

Итак, рассмотрим синхронизацию с помощью световых сигналов. Этот процесс может заключаться, например, в обмене световыми сигналами между двумя удалёнными хронометрами: если сигналы испущены в одно и то же время, то до получения сигнала по каждым часам пройдет одно и то же время. Но ещё проще несколько другой (эквивалентный этому) способ: можно точно в середине отрезка, соединяющего хронометры, произвести вспышку света, и утверждать, что свет придёт к обоим хронометрам одновременно.

В собственной системе отсчёта (в которой хронометры неподвижны) картина симметрична. Однако в любой другой системе отсчёта оба хронометра движутся (для определённости будем считать, что вправо), и тогда свету от середины отрезка, соединяющего их в начальный момент, потребуется меньше времени, чтобы дойти до левого хронометра (движущегося навстречу свету), чем до правого (который импульс света должен догонять).

Таким образом, хронометры, синхронно идущие в собственной системе отсчёта, по часам другой системы отсчёта выглядят несинхронными. Одновременность событий относительна: события, одновременные в одной системе отсчёта, неодновременны в другой.

Несложные геометрические выкладки позволяют (изобразив движение световых импульсов и хронометров на плоскости xt) получить выражение для сдвига начала отсчёта времени:

$-Vx/c^{2}$

(для упрощения мы здесь рассматривали только часы, разнесённые вдоль оси x, но, конечно, всё может быть рассчитано и для общего случая).

Таким образом, сводя вместе результаты пунктов 2 и 3, получаем для преобразования времени

$t'={\frac {t-Vx/c^{2}}{\sqrt {1-V^{2}/c^{2}}}}$.

Данный эффект также можно доказать от противного: если бы он не существовал, или сдвиг начала отсчёта времени не составлял бы $-Vx/c^{2}$, то существовал бы так называемый парадокс близнецов.

Лоренцевское сокращение длины (п.4)

Рассмотрев движение светового импульса вдоль оси x (а не вдоль y, как было в п.1), и потребовав (на основании постулата одинаковости скорости света во всех инерциальных системах отсчёта), чтобы расстояние между двумя точками было всегда равно времени, за которое свет идёт от одной точки до другой, умноженному на (константу) скорость света, можно получить фактор сокращения расстояний вдоль оси x, а учитывая, что смещение начала отсчёта равно $-Vt$, можно получить и преобразование для координаты x:

$x'={\frac {x-Vt}{\sqrt {1-V^{2}/c^{2}}}}.$.

Ещё проще теперь понять, что $x'$ выражается именно таким образом, заметив, что в плоскости $x-ct$ график движения импульса света должен быть прямой, наклонённой под 45° (из-за того, что скорость света — всегда c), а значит и масштаб по осям $x$и $ct$ должен быть одинаковым, а выражения в системе единиц $c=1$ — симметричными.

• Таким образом, преобразования Лоренца достаточно наглядно получаются при коллинеарных пространственных осях. Конечно, возможен и обратный порядок рассуждений: можно сначала получить преобразования Лоренца каким-либо более абстрактным способом, например — одним из упомянутых выше, а потом получить все эффекты, разобранные в этапах данного наглядного доказательства, в качестве простого формального следствия преобразований Лоренца.

Ссылки

• Книга Релятивистский мир